Làm thế nào bạn có thể tìm thấy một hành tinh mới ở ngoại vi Hệ Mặt Trời của chúng ta khi mà chúng quá mờ để có thể nhìn thấy bằng mắt thường và ở rất xa nên nó di chuyển rất chậm giữa các ngôi sao? Đây là vấn đề mà các nhà thiên văn phải đối mặt trong thế kỷ 19 khi họ cố gắng kiểm kê đầy đủ về Hệ Mặt Trời của chúng ta.
Nếu chúng ta có thể nhìn xuống Hệ Mặt Trời từ một nơi nào đó trong không gian ngoài kia, thì việc giải thích chuyển động của các hành tinh sẽ đơn giản hơn nhiều. Nhưng thực tế là, chúng ta phải quan sát vị trí của tất cả các hành tinh khác từ chính hành tinh đang chuyển động của chúng ta. Các nhà khoa học thời Phục hưng không biết chi tiết về chuyển động của Trái Đất hơn gì chuyển động của các hành tinh khác. Vấn đề của họ, như chúng ta đã thấy trong chương Quan sát bầu trời: Sự ra đời của Thiên văn học, là họ phải suy ra bản chất của tất cả chuyển động của hành tinh chỉ bằng cách sử dụng các quan sát trên mặt đất về vị trí của các hành tinh khác trên bầu trời. Để giải quyết vấn đề phức tạp này một cách đầy đủ hơn, cần có những quan sát tốt hơn và những mô hình tốt hơn của hệ hành tinh.

Hình 3.1 Trạm Vũ trụ Quốc tế. Phòng thí nghiệm và là Môi trường sống trong không gian này quay quanh Trái đất 90 phút một lần. (Ảnh: sửa đổi công việc của NASA)
Vào khoảng thời gian Galileo bắt đầu thí nghiệm với các vật thể rơi, những nỗ lực của hai nhà khoa học khác đã nâng cao đáng kể sự hiểu biết của chúng ta về chuyển động của các hành tinh. Hai nhà thiên văn học này là nhà quan sát Tycho Brahe và nhà toán học Johannes Kepler. Họ cùng nhau đặt những suy đoán của Copernicus trên cơ sở toán học đúng đắn và mở đường cho công trình của Isaac Newton trong thế kỷ tiếp theo.
Đài quan sát của Tycho Brahe
Ba năm sau khi tác phẩm De Revolutionibus của Copernicus xuất bản, Tycho Brahe đã chào đời trong một gia đình quý tộc ở Đan Mạch. Ông bắt đầu quan tâm đến thiên văn học và khi còn trẻ, ông đã có những quan sát thiên văn quan trọng. Trong số này có một cuộc nghiên cứu cẩn thận về những gì chúng ta biết ngày nay là một ngôi sao đang nổ tung và phát sáng rực rỡ trên bầu trời đêm. Danh tiếng ngày càng tăng của ông đã giúp ông nhận được sự bảo trợ của Vua Đan Mạch Frederick II, và ở tuổi 30, Brahe đã có thể thiết lập một đài quan sát thiên văn tốt trên đảo Hven ở Biển Bắc (Hình 3.2). Brahe là người cuối cùng và vĩ đại nhất trong số các nhà quan sát tiền kính thiên văn ở châu Âu.
Tại Hven, Brahe đã liên tục ghi lại vị trí của Mặt Trời, Mặt Trăng và các hành tinh trong gần 20 năm. Những quan sát sâu rộng và chính xác của ông đã giúp ông để ý rằng vị trí của các hành tinh khác với vị trí được đưa ra trong các bảng đã xuất bản dựa trên công trình nghiên cứu của Ptolemy. Những dữ liệu này cực kỳ có giá trị, nhưng Brahe không có khả năng phân tích chúng và phát triển một mô hình tốt hơn những gì Ptolemy đã xuất bản. Ông còn bị ức chế hơn nữa vì bản thân là một người khó tính và ngông cuồng, và ông có ngày càng nhiều kẻ thù trong số các quan chức chính phủ. Khi người bảo trợ của ông, Frederick II, qua đời năm 1597, Brahe mất cơ sở chính trị và quyết định rời Đan Mạch. Ông đến cư trú tại Praha, nơi ông trở thành nhà thiên văn của triều đình cho Hoàng đế Rudolf của Bohemia. Ở đó, vào năm trước khi qua đời, Brahe đã tìm thấy một nhà toán học trẻ tuổi có khả năng nhất, Johannes Kepler, để hỗ trợ anh ta trong việc phân tích dữ liệu hành tinh phong phú của mình.

Hình 3.2 Tycho Brahe (1546–1601) và Johannes Kepler (1571–1630). (a) Một bản khắc cách điệu cho thấy Tycho Brahe sử dụng các công cụ của mình để đo độ cao của các thiên thể phía trên đường chân trời. Dụng cụ cong lớn ở phía trước cho phép ông đo các góc chính xác trên bầu trời. Lưu ý rằng khung cảnh này cũng bao gồm những gợi ý về sự hùng vĩ của đài quan sát của Brahe tại Hven. (b) Kepler là một nhà toán học và thiên văn học người Đức. Khám phá của ông về các định luật cơ bản mô tả chuyển động của hành tinh đã đặt thuyết vũ trụ nhật tâm của Copernicus trên một cơ sở toán học vững chắc.
Johannes Kepler
Johannes Kepler sinh ra trong một gia đình nghèo ở tỉnh Württemberg của Đức và sống phần lớn cuộc đời của mình trong cuộc hỗn loạn của Chiến tranh Ba mươi năm (xem Hình 3.2). Ông theo học đại học tại Tubingen và nghiên cứu sự nghiệp thần học. Tại đây, ông học các nguyên lý của hệ thống Copernic và chuyển sang giả thuyết nhật tâm. Cuối cùng, Kepler đến Praha để làm trợ lý cho Brahe, người đã khiến anh phải nỗ lực tìm kiếm một lý thuyết thỏa đáng về chuyển động của hành tinh — một lý thuyết tương thích với chuỗi dài các quan sát được thực hiện tại Hven. Brahe miễn cưỡng cung cấp cho Kepler nhiều tài liệu cùng một lúc vì sợ rằng Kepler sẽ tự mình khám phá ra bí mật của chuyển động vũ trụ, từ đó cướp đi một phần vinh quang của Brahe. Chỉ sau cái chết của Brahe vào năm 1601, Kepler mới được sở hữu đầy đủ những kỷ lục vô giá. Nghiên cứu của chúng chiếm phần lớn thời gian của Kepler trong hơn 20 năm.
Thông qua phân tích chuyển động của các hành tinh, Kepler đã phát triển một loạt các nguyên tắc, ngày nay được gọi là ba định luật Kepler, mô tả hoạt động của các hành tinh dựa trên đường đi của chúng trong không gian. Hai định luật đầu tiên về chuyển động của hành tinh được xuất bản năm 1609 trên tạp chí The New Astronomy. Khám phá của họ là một bước tiến sâu sắc trong sự phát triển của khoa học hiện đại.
Hai định luật đầu tiên của chuyển động hành tinh
Đường đi của một vật trong không gian được gọi là quỹ đạo của nó. Ban đầu Kepler cho rằng quỹ đạo của các hành tinh là những vòng tròn, nhưng làm như vậy không cho phép ông tìm thấy những quỹ đạo phù hợp với những quan sát của Brahe. Làm việc với dữ liệu cho Sao Hỏa, cuối cùng ông phát hiện ra rằng quỹ đạo của hành tinh đó có hình dạng là một hình tròn hơi dẹt, hoặc hình elip. Bên cạnh đường tròn, đường elip là loại đường cong khép kín đơn giản nhất, thuộc họ đường cong được gọi là mặt cắt hình nón (Hình 3.3).
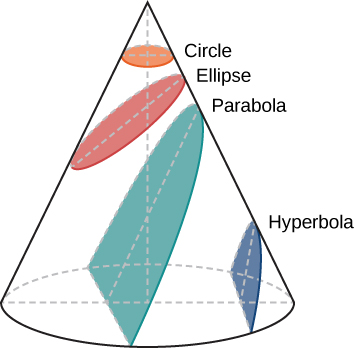
Hình 3.3 Mặt cắt hình nón. Đường tròn, elip, parabol và hyperbol đều được tạo thành bởi giao của một mặt phẳng với một hình nón. Đây là lý do tại sao những đường cong như vậy được gọi là mặt cắt hình nón.
Bạn có thể nhớ lại từ các lớp học toán rằng trong một vòng tròn, tâm là một điểm đặc biệt. Khoảng cách từ tâm đến bất kỳ vị trí nào trên vòng tròn là hoàn toàn giống nhau. Trong một hình elip, tổng khoảng cách từ hai điểm đặc biệt bên trong elip đến một điểm bất kỳ trên elip luôn bằng nhau. Hai điểm bên trong hình elip này được gọi là tiêu điểm (focus, số nhiều: foci), một từ được phát minh cho mục đích này bởi Kepler.
Thuộc tính này gợi ý một cách đơn giản để vẽ một hình elip (Hình 3.4). Chúng ta quấn các đầu của một vòng dây quanh hai chiếc đinh ghim đẩy qua một tờ giấy vào bảng vẽ, để dây được chùng xuống. Nếu chúng ta ấn bút chì vào sợi dây, làm cho sợi dây căng ra, rồi trượt bút chì kéo căng sợi dây xung quanh chỗ đinh ghim, thì đường cong tạo ra là một hình elip. Tại bất kỳ điểm nào mà bút chì đặt lên, tổng khoảng cách từ bút chì đến hai đinh ghim là một độ dài không đổi — chính là độ dài của đoạn dây. Các đinh ghim nằm ở hai tiêu điểm của hình elip.
Đường kính rộng nhất của hình elip được gọi là trục chính (major axis) của nó. Một nửa khoảng cách này — nghĩa là, khoảng cách từ tâm của hình elip đến một đầu — là bán trục lớn (semimajor axis), thường được sử dụng để chỉ định kích thước của hình elip. Ví dụ, bán trục lớn của quỹ đạo Sao Hỏa, cũng là khoảng cách trung bình của hành tinh này từ Mặt Trời, là 228 triệu km.
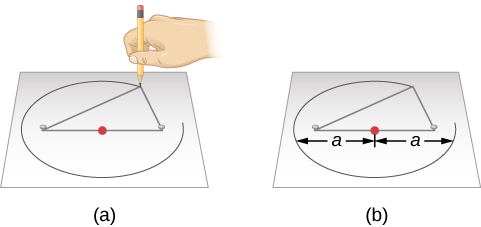
Hình 3.4 Vẽ một hình Elip. (a) Chúng ta có thể tạo một hình elip bằng cách đẩy hai cái đinh (các vật màu trắng) vào một mảnh giấy trên bảng vẽ, rồi vòng một sợi dây quanh cái đinh. Mỗi mũi đinh đại diện cho một tiêu điểm của hình elip, với một trong hai đinh ghim là Mặt Trời. Dùng bút chì kéo căng sợi dây rồi di chuyển bút chì xung quanh đinh ghim. Chiều dài của sợi dây không đổi, do đó tổng khoảng cách từ bất kỳ điểm nào trên elip đến hai tiêu điểm luôn không đổi. (b) Trong hình minh họa này, mỗi bán trục lớn được ký hiệu bằng a. Khoảng cách 2a được gọi là trục chính của elip.
Hình dạng (độ tròn) của một hình elip phụ thuộc vào mức độ gần nhau của hai tiêu điểm so với trục chính. Tỷ số giữa khoảng cách giữa các tiêu điểm và độ dài của trục chính được gọi là độ lệch tâm (eccentricity) của elip.
Nếu các tiêu điểm (hoặc các điểm đinh ghim) được di chuyển đến cùng một vị trí, thì khoảng cách giữa các tiêu điểm sẽ bằng không. Điều này có nghĩa là độ lệch tâm bằng 0 và hình elip chỉ là một hình tròn; do đó, một hình tròn có thể được gọi là một hình elip có độ lệch tâm bằng không. Trong một hình tròn, bán trục lớn sẽ là bán kính.
Tiếp theo, chúng ta có thể tạo các hình elip với nhiều độ dài khác nhau (hoặc độ dài mở rộng) bằng cách thay đổi khoảng cách của các đinh ghim (miễn là chúng không cách xa nhau hơn độ dài của dây). Độ lệch tâm càng lớn thì hình elip càng dài ra, độ lệch tâm tối đa là 1,0, khi hình elip trở nên "phẳng", cực khác so với đường tròn.
Kích thước và hình dạng của hình elip hoàn toàn được xác định bởi trục bán kính và độ lệch tâm của nó. Sử dụng dữ liệu của Brahe, Kepler nhận thấy rằng Sao Hỏa có quỹ đạo hình elip, với Mặt Trời ở một tiêu điểm (tiêu điểm còn lại là trống). Độ lệch tâm của quỹ đạo Sao Hỏa chỉ khoảng 0,1; quỹ đạo của nó, được vẽ theo tỷ lệ, thực tế sẽ không thể phân biệt được với một vòng tròn, nhưng sự khác biệt hóa ra là rất quan trọng để hiểu chuyển động của các hành tinh.
Kepler đã khái quát kết quả này trong định luật đầu tiên của mình và nói rằng quỹ đạo của tất cả các hành tinh đều là hình elip. Đây là một thời điểm quyết định trong lịch sử tư tưởng nhân loại: không nhất thiết phải chỉ có các vòng tròn để có một vũ trụ có thể chấp nhận được. Vũ trụ có thể phức tạp hơn một chút so với mong muốn của các nhà triết học Hy Lạp.
Định luật thứ hai của Kepler đề cập đến tốc độ mà mỗi hành tinh di chuyển dọc theo hình elip của nó, còn được gọi là tốc độ quỹ đạo của nó. Làm việc với các quan sát của Brahe về Sao Hỏa, Kepler phát hiện ra rằng hành tinh này tăng tốc khi nó đến gần Mặt Trời và chậm lại khi nó rời khỏi Mặt Trời. Ông thể hiện dạng chính xác của mối quan hệ này bằng cách tưởng tượng rằng Mặt Trời và Sao Hỏa được nối với nhau bằng một đường thẳng đàn hồi. Khi Sao Hỏa ở gần Mặt Trời hơn (vị trí 1 và 2 trong Hình 3.5), đường đàn hồi không bị giãn ra nhiều và hành tinh chuyển động nhanh dần đều. Xa hơn Mặt Trời, như ở vị trí 3 và 4, đường thẳng bị kéo dài ra rất nhiều, và hành tinh không di chuyển nhanh như vậy. Khi sao Hỏa di chuyển trong quỹ đạo hình elip quanh Mặt Trời, đường đàn hồi quét ra các vùng của elip khi nó di chuyển (các vùng có màu trong hình của chúng ta). Kepler nhận thấy rằng trong những khoảng thời gian bằng nhau (t), diện tích bị quét ra trong không gian bởi đường tưởng tượng này luôn bằng nhau; nghĩa là diện tích vùng B từ 1 đến 2 bằng diện tích vùng A từ 3 đến 4.
Nếu một hành tinh chuyển động theo quỹ đạo tròn thì dây đàn hồi luôn bị kéo căng một lượng như nhau và hành tinh đó chuyển động với vận tốc không đổi quanh quỹ đạo của nó. Nhưng, như Kepler đã phát hiện ra, trong hầu hết các quỹ đạo, tốc độ của một hành tinh quay quanh ngôi sao của nó (hoặc mặt trăng quay quanh hành tinh của nó) có xu hướng thay đổi vì quỹ đạo là hình elip.
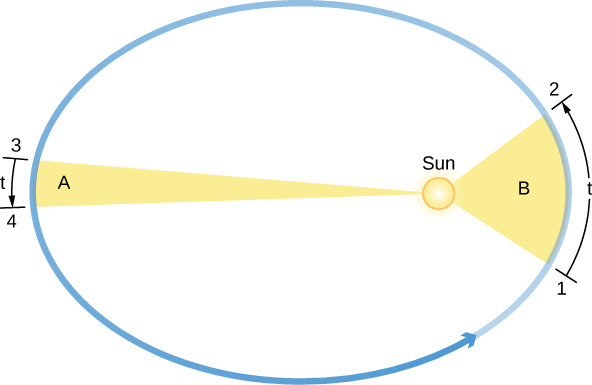
Hình 3.5 Định luật thứ hai của Kepler: Quy luật về các diện tích bằng nhau. Tốc độ quỹ đạo của một hành tinh di chuyển quanh Mặt Trời (vật thể tròn bên trong hình elip) thay đổi theo cách mà trong những khoảng thời gian bằng nhau (t), đường thẳng giữa Mặt Trời và một hành tinh quét ra những khu vực bằng nhau (A và B) . Lưu ý rằng độ lệch tâm của quỹ đạo của các hành tinh trong Hệ Mặt Trời của chúng ta về cơ bản ít hơn đáng kể so với hình minh họa ở đây.
LIÊN KẾT ĐỂ HỌC
Trình biểu diễn Định luật thứ hai của Kepler từ dự án ScienceSims của CCNY cho thấy cách một hành tinh quay quanh quét ra cùng một khu vực trong cùng một thời điểm.
Định luật thứ ba của Kepler
Hai định luật đầu tiên của Kepler về chuyển động của hành tinh mô tả hình dạng quỹ đạo của một hành tinh và cho phép chúng ta tính toán tốc độ chuyển động của nó tại bất kỳ điểm nào trên quỹ đạo. Kepler rất vui vì đã khám phá ra các quy tắc cơ bản như vậy, nhưng chúng không đáp ứng được nhiệm vụ tìm hiểu đầy đủ chuyển động của các hành tinh của ông. Ông muốn biết tại sao quỹ đạo của các hành tinh lại có khoảng cách như vậy và để tìm ra một mô hình toán học trong chuyển động của chúng — một “sự hài hòa của các quả cầu” như cách gọi của ông. Trong nhiều năm, ông đã làm việc để khám phá các mối quan hệ toán học chi phối khoảng cách giữa các hành tinh và thời gian mỗi hành tinh quay quanh Mặt Trời.
Năm 1619, Kepler phát hiện ra một mối quan hệ cơ bản để liên hệ quỹ đạo của các hành tinh với khoảng cách tương đối của chúng từ Mặt Trời. Chúng ta xác định chu kỳ quỹ đạo của hành tinh, (P), là thời gian hành tinh đó đi một lần quanh Mặt Trời. Ngoài ra, hãy nhớ lại rằng bán trục lớn của một hành tinh, a, bằng khoảng cách trung bình của nó từ Mặt Trời. Mối quan hệ, hiện được gọi là định luật thứ ba của Kepler, nói rằng bình phương chu kỳ quỹ đạo của một hành tinh tỷ lệ với lập phương bán trục lớn của quỹ đạo của nó, hoặc
𝑃2 ∝ 𝑎3
Khi P (chu kỳ quỹ đạo) được đo bằng năm và a được biểu thị bằng một đại lượng được gọi là đơn vị thiên văn (AU), hai vế của công thức không chỉ tỷ lệ mà còn bằng nhau. Một AU là khoảng cách trung bình giữa Trái Đất và Mặt Trời và xấp xỉ bằng 1,5×108 km. Trong các đơn vị này,
𝑃2 = 𝑎3
Định luật thứ ba của Kepler áp dụng cho tất cả các vật thể quay quanh Mặt Trời, bao gồm cả Trái Đất, và cung cấp một phương tiện để tính toán khoảng cách tương đối của chúng với Mặt Trời từ thời gian chúng di chuyển trên quỹ đạo. Hãy xem một ví dụ cụ thể để minh họa định luật thứ ba của Kepler hữu ích như thế nào.
Ví dụ, giả sử bạn tính thời gian Sao Hỏa quay quanh Mặt Trời (tính bằng năm Trái Đất). Khi đó, định luật thứ ba của Kepler có thể được sử dụng để tính khoảng cách trung bình của Sao Hỏa từ Mặt Trời. Bình phương chu kỳ quỹ đạo của Sao Hỏa (1,88 năm Trái Đất), hay P2, là 1,882 = 3,53 và theo phương trình cho định luật thứ ba của Kepler, điều này bằng lập phương của bán trục lớn, hoặc a3. Vậy, con số nào phải được lập phương để có kết quả là 3,53? Câu trả lời là 1,52 (vì 1,52×1,52×1,52=3,53). Do đó, bán trục lớn của Sao Hỏa tính theo đơn vị thiên văn phải là 1,52 AU. Nói cách khác, để quay quanh Mặt Trời trong vòng chưa đầy hai năm, Sao Hỏa phải cách xa Mặt Trời hơn khoảng 50% (gấp rưỡi) so với Trái đất.
VÍ DỤ 3.1 Tính toán chu kỳ quỹ đạo
Ví dụ 1
Hãy tưởng tượng một vật thể đang di chuyển quanh Mặt Trời. Chu kỳ quỹ đạo của vật thể sẽ là bao nhiêu nếu quỹ đạo của nó có bán trục lớn là 50 AU?
Đáp án
Từ định luật thứ ba của Kepler, chúng tôi biết rằng (khi chúng tôi sử dụng đơn vị năm và AU)
𝑃2 = 𝑎3
Nếu quỹ đạo của vật thể có bán trục lớn là 50 AU (a = 50), chúng ta có thể lập phương 50 và sau đó lấy căn bậc hai của kết quả để nhận được P:
Do đó, chu kỳ quỹ đạo của vật thể là khoảng 350 năm. Điều này sẽ đặt vật thể giả định của chúng ta vượt ra ngoài quỹ đạo của Sao Diêm Vương.
Ví dụ 2
Chu kỳ quỹ đạo của một tiểu hành tinh (một khối đá nằm giữa Sao Hỏa và Sao Mộc) có bán trục lớn là 3 AU sẽ như thế nào?
Đáp án
Ba định luật chuyển động hành tinh của Kepler có thể được tóm tắt như sau:
- Định luật đầu tiên của Kepler: Mỗi hành tinh chuyển động quanh Mặt Trời theo quỹ đạo là một hình elip, với Mặt Trời tại một tiêu điểm của hình elip.
- Định luật thứ hai của Kepler: Đường thẳng nối một hành tinh và Mặt Trời quét ra các khu vực bằng nhau trong không gian trong những khoảng thời gian bằng nhau.
- Định luật thứ ba của Kepler: Bình phương của chu kỳ quỹ đạo của hành tinh tỷ lệ thuận với lập phương của bán trục lớn trên quỹ đạo của nó.
Ba định luật của Kepler cung cấp một mô tả hình học chính xác về chuyển động của hành tinh trong khuôn khổ của hệ Copernic. Với những công cụ này, người ta có thể tính toán các vị trí hành tinh với độ chính xác được cải thiện đáng kể. Tuy nhiên, các định luật của Kepler hoàn toàn mang tính mô tả: chúng không giúp chúng ta hiểu được lực tự nhiên nào buộc các hành tinh tuân theo bộ quy tắc cụ thể này. Bước đó đã được giao cho Isaac Newton.
VÍ DỤ 3.2 Áp dụng Luật thứ ba của Kepler
Ví dụ 1
Sử dụng chu kỳ quỹ đạo và bán trục lớn của Sao Kim và Trái Đất được cung cấp ở đây, tính P2 và a3, đồng thời xác minh rằng chúng tuân theo định luật thứ ba của Kepler. Chu kỳ quỹ đạo của sao Kim là 0,62 năm, và bán trục lớn của nó là 0,72 AU. Chu kỳ quỹ đạo của Trái Đất là 1,00 năm và bán trục lớn của nó là 1,00 AU.
Đáp án
Chúng ta có thể sử dụng phương trình cho định luật thứ ba của Kepler, P2∝a3. Đối với Sao Kim, P2=0,62×0,62=0,38 và a3=0,72×0,72×0,72=0,37 (các con số làm tròn đôi khi gây ra sự khác biệt nhỏ như thế này). Bình phương của chu kỳ quỹ đạo (0,38) xấp xỉ lập phương của bán trục lớn (0,37). Do đó, Sao Kim tuân theo định luật thứ ba của Kepler. Đối với Trái Đất, P2=1,00×1,00=1,00 và a3=1,00×1,00×1,00=1,00. Bình phương của chu kỳ quỹ đạo (1,00) xấp xỉ (trong trường hợp này, bằng) hình lập phương của trục bán nguyệt (1,00). Do đó, Trái đất tuân theo định luật thứ ba của Kepler.
Ví dụ 2
Sử dụng các chu kỳ quỹ đạo và trục bán tinh của Sao Thổ và Sao Mộc được cung cấp ở đây, tính P2 và a3, đồng thời xác minh rằng chúng tuân theo định luật thứ ba của Kepler. Chu kỳ quỹ đạo của Sao Thổ là 29,46 năm và bán trục lớn của nó là 9,54 AU. Chu kỳ quỹ đạo của Sao Mộc là 11,86 năm và bán trục lớn của nó là 5,20 AU.
Đáp án
Đối với sao Thổ, P2=29,46×29,46=867,9 và a3=9,54×9,54×9,54=868,3. Bình phương của chu kỳ quỹ đạo (867,9) xấp xỉ với lập phương của bán trục lớn (868,3). Do đó, Sao Thổ tuân theo định luật thứ ba của Kepler.
LIÊN KẾT ĐỂ HỌC
Để vinh danh nhà khoa học đầu tiên phát minh ra các định luật chi phối chuyển động của các hành tinh, nhóm chế tạo tàu vũ trụ đầu tiên để tìm kiếm các hành tinh quay quanh các ngôi sao khác đã quyết định đặt tên cho tàu thăm dò là “Kepler”. Truy cập trang web Kepler của NASA để tìm hiểu thêm về cuộc đời của Johannes Kepler và các định luật chuyển động của các hành tinh của ông. Trang web Kepler của NASA và theo các liên kết mà bạn quan tâm.
(còn tiếp...)
Tham khảo
- Astronomy 1st edition, Senior Contributing Authors: A. Franknoi, D. Morrison, S. Wolff ©2017 Rice University, Textbook content produced by OpenStax is licensed under a Creative Commons Attribution 4.0 International License. (Access for free at https://openstax.org/details/books/astronomy




![[RECAP SỰ KIỆN] LỚP HỌC THIÊN VĂN: CÙNG NCS. NGUYỄN BÌNH NGƯỢC DÒNG THỜI GIAN,](/images/Content_Images/2025/2025-09/LHTV_NB_01.jpg#joomlaImage://local-images/Content_Images/2025/2025-09/LHTV_NB_01.jpg?width=2000&height=1253)


